Junção de tabelas com um identificador comum
By Ricardo de Oliveira Perdiz
April 23, 2020
Postagem preparada em versão reduzida para a disciplina BOT-89 Introdução ao R e Preparação de Dados, ligada ao Programa de Pós-graduação em Ciências Biológicas (Botânica) (PPGBOT) do Instituto Nacional de Pesquisas da Amazônia (INPA), Amazonas, Brasil, e ministrada anualmente pelo Dr. Alberto Vicentini (INPA).
Unir tabelas é uma prática corriqueira com bases de dados.
Para unir tabelas, é necessário que duas tabelas diferentes possuam uma coluna em comum, a quem vamos chamar de identificador.
O pacote base do R fornece uma função que executa essa ação, chamada merge().
Porém, há alguns tipos de junções não podem ser executados com esta função, o que nos levará ao uso de vetores lógicos em conjunto com a função interaction().
Mostraremos exemplos com essas duas maneiras.
Dados para nossa prática
Utilizaremos três tabelas para esta prática:
- O
data.frametab1possui nomes de famílias, gêneros e epítetos específicos de algumas angiospermas:
familia <- c("Burseraceae", "Solanaceae","Sapindaceae", "Rubiaceae", "Lauraceae")
generos <- c("Protium", "Trattinnickia", "Dacryodes", "Duckeodendron", "Markea", "Solanum", "Allophylastrum", "Cupania", "Thinouia", "Psychotria", "Duroia", "Cinchona", "Ocotea", "Licaria", "Rhodostemonodaphne", "Anisophyllea", "Freziera")
epitetos <- c("aracouchini", "burserifolia", "edilsonii", "cestroides", "ulei", "cyathophorum", "frutescens", "rubiginosa", "myriantha", "viridis", "eriopila", "amazonica", "delicata", "aureosericea","recurva", "manausensis", "carinata")
tab1 <- data.frame(familia = c(rep(familia, each = 3), "Anisophylleaceae", "Pentaphylacaceae"), genero = generos, epiteto = epitetos, stringsAsFactors = FALSE)
| familia | genero | epiteto |
|---|---|---|
| Burseraceae | Protium | aracouchini |
| Burseraceae | Trattinnickia | burserifolia |
| Burseraceae | Dacryodes | edilsonii |
| Solanaceae | Duckeodendron | cestroides |
| Solanaceae | Markea | ulei |
| Solanaceae | Solanum | cyathophorum |
| Sapindaceae | Allophylastrum | frutescens |
| Sapindaceae | Cupania | rubiginosa |
| Sapindaceae | Thinouia | myriantha |
| Rubiaceae | Psychotria | viridis |
| Rubiaceae | Duroia | eriopila |
| Rubiaceae | Cinchona | amazonica |
| Lauraceae | Ocotea | delicata |
| Lauraceae | Licaria | aureosericea |
| Lauraceae | Rhodostemonodaphne | recurva |
| Anisophylleaceae | Anisophyllea | manausensis |
| Pentaphylacaceae | Freziera | carinata |
- O
data.frametab2contem um conjunto pequeno com alguns nomes de famílias, gêneros, e o nome de seus respectivos clados acima dos nomes de ordens segundo o APG (2016):
familia2 <- c("Burseraceae", "Solanaceae","Sapindaceae", "Rubiaceae", "Annonaceae")
generos2 <- c("Protium", "Duckeodendron", "Thinouia", "Psychotria", "Guatteria")
clado <- c("Malvids", "Lamiids", "Malvids", "Lamiids", "Magnoliids")
tab2 <- data.frame(familia = familia2, genero = generos2, clado = clado, stringsAsFactors = FALSE)
| familia | genero | clado |
|---|---|---|
| Burseraceae | Protium | Malvids |
| Solanaceae | Duckeodendron | Lamiids |
| Sapindaceae | Thinouia | Malvids |
| Rubiaceae | Psychotria | Lamiids |
| Annonaceae | Guatteria | Magnoliids |
- O
data.frametab3corresponde à tabela 2,tab2, sem as famílias Solanaceae e Rubiaceae:
tab3 <- subset(tab1, familia %in% c("Burseraceae", "Sapindaceae"))
| familia | genero | epiteto |
|---|---|---|
| Burseraceae | Protium | aracouchini |
| Burseraceae | Trattinnickia | burserifolia |
| Burseraceae | Dacryodes | edilsonii |
| Sapindaceae | Allophylastrum | frutescens |
| Sapindaceae | Cupania | rubiginosa |
| Sapindaceae | Thinouia | myriantha |
Unindo tabelas com merge()
O básico para entender a função merge() é saber que existem dois argumentos, x e y, que correspondem aos data.frames de entrada.
Quando unimos tabelas, existem junções que adicionam variáveis, e junções que filtram variáveis.
Vamos ver abaixo 4 tipos da primeira (
junção interna,
junção à esquerda,
junção à direita,
junção total), e dois tipos desta última (
semijunção e
antijunção).
Junção interna
ao juntarmos tabelas
xey, temos todas as linhas dexem que há valores em comum comy, e todas as colunas dexey. Se houver múltiplas correspondências entrexey, todas as combinações retornam.
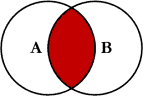
Em nosso exemplo, vamos unir as tabelas 1 e 2.
Ambas possuem em comum os identificadores familia e genero.
Para facilitar o entendimento, vamos verificar primeiro cada tabela com cores para checar as correspondências entre x e y nas variáveis em comum:
| familia | genero | epiteto |
|---|---|---|
| Burseraceae | Protium | aracouchini |
| Burseraceae | Trattinnickia | burserifolia |
| Burseraceae | Dacryodes | edilsonii |
| Solanaceae | Duckeodendron | cestroides |
| Solanaceae | Markea | ulei |
| Solanaceae | Solanum | cyathophorum |
| Sapindaceae | Allophylastrum | frutescens |
| Sapindaceae | Cupania | rubiginosa |
| Sapindaceae | Thinouia | myriantha |
| Rubiaceae | Psychotria | viridis |
| Rubiaceae | Duroia | eriopila |
| Rubiaceae | Cinchona | amazonica |
| Lauraceae | Ocotea | delicata |
| Lauraceae | Licaria | aureosericea |
| Lauraceae | Rhodostemonodaphne | recurva |
| Anisophylleaceae | Anisophyllea | manausensis |
| Pentaphylacaceae | Freziera | carinata |
| familia | genero | clado |
|---|---|---|
| Burseraceae | Protium | Malvids |
| Solanaceae | Duckeodendron | Lamiids |
| Sapindaceae | Thinouia | Malvids |
| Rubiaceae | Psychotria | Lamiids |
| Annonaceae | Guatteria | Magnoliids |
Reparem que os valores em que há correspondência entre x e y estão coloridos de amarelo; para os em que não há correspondência, estão coloridos de vermelho.
Agora, executemos a junção das duas tabelas:
merge(x = tab1, y = tab2)
## familia genero epiteto clado
## 1 Burseraceae Protium aracouchini Malvids
## 2 Rubiaceae Psychotria viridis Lamiids
## 3 Sapindaceae Thinouia myriantha Malvids
## 4 Solanaceae Duckeodendron cestroides Lamiids
Vejam que houve a incorporação dos valores da coluna epiteto, presente apenas na tabela 2, em que há correspondência entre as tabelas 1 e 2.
É importante notar que as famílias Lauraceae, Anisophylleaceae, e Pentaphylacaceae ficaram de fora, pois não são encontradas na tabela y, isto é, a tabela 2, assim como seus respectivos gêneros e epítetos associados a estes.
Gêneros presentes na tabela 1 de famílias em comum entre ambas as tabelas também não foram incorporados nessa junção, pois nãp encontram correspondência na tabela 2: Dacryodes, Trattinnickia, Markea, Solanum, Allophylastrum, Cupania, Duroia, Cinchona.
Revejam o conceito de
junção interna para entender o porquê desse acontecimento.
Junção à esquerda
ao juntarmos tabelas
xey, temos todas as linhas dex, e todas as colunas dexey. Linhas emxsem correspência emyterão valoresNAadicionados nas novas colunas. Se houver múltiplas correspondências entrexey, todas as combinações retornam.
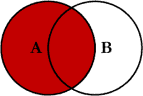
Continuaremos utilizando as tabelas 1 e 2.
Como mostrado anteriormente, ambas possuem em comum os identificadores familia e genero.
Chequemos novamente as cores das correspondências dentro de cada identificador, coloridas em amarelo:
| familia | genero | epiteto |
|---|---|---|
| Burseraceae | Protium | aracouchini |
| Burseraceae | Trattinnickia | burserifolia |
| Burseraceae | Dacryodes | edilsonii |
| Solanaceae | Duckeodendron | cestroides |
| Solanaceae | Markea | ulei |
| Solanaceae | Solanum | cyathophorum |
| Sapindaceae | Allophylastrum | frutescens |
| Sapindaceae | Cupania | rubiginosa |
| Sapindaceae | Thinouia | myriantha |
| Rubiaceae | Psychotria | viridis |
| Rubiaceae | Duroia | eriopila |
| Rubiaceae | Cinchona | amazonica |
| Lauraceae | Ocotea | delicata |
| Lauraceae | Licaria | aureosericea |
| Lauraceae | Rhodostemonodaphne | recurva |
| Anisophylleaceae | Anisophyllea | manausensis |
| Pentaphylacaceae | Freziera | carinata |
| familia | genero | clado |
|---|---|---|
| Burseraceae | Protium | Malvids |
| Solanaceae | Duckeodendron | Lamiids |
| Sapindaceae | Thinouia | Malvids |
| Rubiaceae | Psychotria | Lamiids |
| Annonaceae | Guatteria | Magnoliids |
Em uma junção à esquerda, todas as linhas de x retornam após a junção.
Para executar este tipo de junção, acrescentaremos um novo argumento, all.x = TRUE, indicando que manteremos todas as linhas de x, isto é, o data.frame à esquerda, que é a tabela 1.
merge(x = tab1, y = tab2, all.x = TRUE)
## familia genero epiteto clado
## 1 Anisophylleaceae Anisophyllea manausensis <NA>
## 2 Burseraceae Dacryodes edilsonii <NA>
## 3 Burseraceae Protium aracouchini Malvids
## 4 Burseraceae Trattinnickia burserifolia <NA>
## 5 Lauraceae Licaria aureosericea <NA>
## 6 Lauraceae Ocotea delicata <NA>
## 7 Lauraceae Rhodostemonodaphne recurva <NA>
## 8 Pentaphylacaceae Freziera carinata <NA>
## 9 Rubiaceae Cinchona amazonica <NA>
## 10 Rubiaceae Duroia eriopila <NA>
## 11 Rubiaceae Psychotria viridis Lamiids
## 12 Sapindaceae Allophylastrum frutescens <NA>
## 13 Sapindaceae Cupania rubiginosa <NA>
## 14 Sapindaceae Thinouia myriantha Malvids
## 15 Solanaceae Duckeodendron cestroides Lamiids
## 16 Solanaceae Markea ulei <NA>
## 17 Solanaceae Solanum cyathophorum <NA>
Agora, temos uma nova situação. Para os valores de x sem correspondência em y, valores NA são acrescentados.
Reparem na coluna clado e vejam que isso ocorreu apenas nesta variável.
Por exemplo, vejam a família Anisophylleaceae. Ela ocorre apenas na tabela 1 e, portanto, não possui nenhum valor de cladoa ssociado a ela, pois esta variável ocorre apenas na tabela 2. Com a junção das tabelas, essa variável é retida, porém sem a existência de um valor para a família, é inserido então o valor NA.
Temos também o caso de Annonaceae, presente na tabela 2. A família não é recuperada na junção interna, pois ela não existe na tabela 1 dentro da variável familia e, portanto, não apresenta correspondência com nenhum dado da tabela 1.
Revejam o conceito de
junção à esquerda para entender o porquê desse acontecimento.
Junção à direita
ao juntarmos tabelas
xey, temos todas as linhas dey, e todas as colunas dexey.Linhas emysem correspência emxterão valores NA adicionados nas novas colunas. Se houver múltiplas correspondências entrexey, todas as combinações retornam.
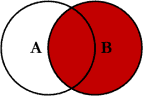
De maneira oposta à junção à esquerda, na junção à direita são mantidas todas as linhas de y.
Desta vez, o argumento a ser utilizado é all.y = TRUE.
Antes de executar a junção, vamos checar novamente as variáveis em comum e correspondências entre as tabelas x e y:
| familia | genero | epiteto |
|---|---|---|
| Burseraceae | Protium | aracouchini |
| Burseraceae | Trattinnickia | burserifolia |
| Burseraceae | Dacryodes | edilsonii |
| Solanaceae | Duckeodendron | cestroides |
| Solanaceae | Markea | ulei |
| Solanaceae | Solanum | cyathophorum |
| Sapindaceae | Allophylastrum | frutescens |
| Sapindaceae | Cupania | rubiginosa |
| Sapindaceae | Thinouia | myriantha |
| Rubiaceae | Psychotria | viridis |
| Rubiaceae | Duroia | eriopila |
| Rubiaceae | Cinchona | amazonica |
| Lauraceae | Ocotea | delicata |
| Lauraceae | Licaria | aureosericea |
| Lauraceae | Rhodostemonodaphne | recurva |
| Anisophylleaceae | Anisophyllea | manausensis |
| Pentaphylacaceae | Freziera | carinata |
| familia | genero | clado |
|---|---|---|
| Burseraceae | Protium | Malvids |
| Solanaceae | Duckeodendron | Lamiids |
| Sapindaceae | Thinouia | Malvids |
| Rubiaceae | Psychotria | Lamiids |
| Annonaceae | Guatteria | Magnoliids |
Agora executaremos a junção com o comando abaixo. Não deixem de reparar no uso do argumento all.y = TRUE, pois ele é o responsável por agora manter todas as linhas da tabela 2 (== y):
merge(x = tab1, y = tab2, all.y = TRUE)
## familia genero epiteto clado
## 1 Annonaceae Guatteria <NA> Magnoliids
## 2 Burseraceae Protium aracouchini Malvids
## 3 Rubiaceae Psychotria viridis Lamiids
## 4 Sapindaceae Thinouia myriantha Malvids
## 5 Solanaceae Duckeodendron cestroides Lamiids
Notem que agora todos os dados da tabela 2 foram mantidos.
Houve a inserção de um valor NA para a família Annonaceae na variável epiteto, pois esta variável não está presente na tabela 2.
Revejam o conceito de
junção à direita para entender o porquê desse acontecimento.
Junção total
ao juntarmos tabelas
xey, temos todas as linhas e colunas dexey. Onde não houver valores correspondentes, valoresNAserão colocados nesses lugares.
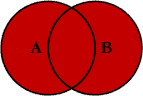
Em uma junção total, uniremos todas as linha de x e y utilizando o argumento all = TRUE.
merge(x = tab1, y = tab2, all = TRUE)
## familia genero epiteto clado
## 1 Anisophylleaceae Anisophyllea manausensis <NA>
## 2 Annonaceae Guatteria <NA> Magnoliids
## 3 Burseraceae Dacryodes edilsonii <NA>
## 4 Burseraceae Protium aracouchini Malvids
## 5 Burseraceae Trattinnickia burserifolia <NA>
## 6 Lauraceae Licaria aureosericea <NA>
## 7 Lauraceae Ocotea delicata <NA>
## 8 Lauraceae Rhodostemonodaphne recurva <NA>
## 9 Pentaphylacaceae Freziera carinata <NA>
## 10 Rubiaceae Cinchona amazonica <NA>
## 11 Rubiaceae Duroia eriopila <NA>
## 12 Rubiaceae Psychotria viridis Lamiids
## 13 Sapindaceae Allophylastrum frutescens <NA>
## 14 Sapindaceae Cupania rubiginosa <NA>
## 15 Sapindaceae Thinouia myriantha Malvids
## 16 Solanaceae Duckeodendron cestroides Lamiids
## 17 Solanaceae Markea ulei <NA>
## 18 Solanaceae Solanum cyathophorum <NA>
Reparem que valores NA são colocados nos valores da tabela 2 referentes à coluna epiteto, ausente na tabela 1.
O mesmo se passa com valores da coluna clado, presente na tabela 2 e ausente na tabela 1.
Revejam o conceito de
junção total para entender o porquê desse acontecimento.
Semijunção
ao juntarmos tabelas
xey, temos todas as linhas dexonde houver valores correspondentes emy, mantendo apenas colunas dex. É parecida com a junção interna, porém difere desta por nunca duplicar valores dex, retornando sempre apenas valores dexque houver uma correspondência emy.
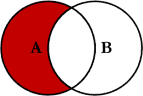
A semijunção é muito similar à junção interna, diferindo desta por não incorporar as colunas de y, pois apenas utiliza esta tabela para filtrar os dados de x, constituindo-se então em um tipo de junção que filtra variáveis.
Neste exemplo, utilizaremos as tabelas 1 e 3.
Ambas compartilham as colunas familia e genero.
Vamos checar primeiramente cada tabela e ver o que é compartilhado entre cada uma:
| familia | genero | epiteto |
|---|---|---|
| Burseraceae | Protium | aracouchini |
| Burseraceae | Trattinnickia | burserifolia |
| Burseraceae | Dacryodes | edilsonii |
| Solanaceae | Duckeodendron | cestroides |
| Solanaceae | Markea | ulei |
| Solanaceae | Solanum | cyathophorum |
| Sapindaceae | Allophylastrum | frutescens |
| Sapindaceae | Cupania | rubiginosa |
| Sapindaceae | Thinouia | myriantha |
| Rubiaceae | Psychotria | viridis |
| Rubiaceae | Duroia | eriopila |
| Rubiaceae | Cinchona | amazonica |
| Lauraceae | Ocotea | delicata |
| Lauraceae | Licaria | aureosericea |
| Lauraceae | Rhodostemonodaphne | recurva |
| Anisophylleaceae | Anisophyllea | manausensis |
| Pentaphylacaceae | Freziera | carinata |
| familia | genero | epiteto |
|---|---|---|
| Burseraceae | Protium | aracouchini |
| Burseraceae | Trattinnickia | burserifolia |
| Burseraceae | Dacryodes | edilsonii |
| Sapindaceae | Allophylastrum | frutescens |
| Sapindaceae | Cupania | rubiginosa |
| Sapindaceae | Thinouia | myriantha |
Para executar uma semijunção com o pacote base do R, devemos fazer uso de vetores lógicos e da função interaction(), pois a função merge() não fornece uma maneira de se obter o que desejamos.
Vamos então à prática1.
As colunas compartilhadas por ambas as tabelas serão nossas chaves:
chaves <- c("familia", "genero")
Partimos então para filtrar na tabela 1 a combinação de linhas para esse conjunto de colunas utilizando a função interaction() do pacote base do R:
interaction(tab1[, chaves])
## [1] Burseraceae.Protium Burseraceae.Trattinnickia
## [3] Burseraceae.Dacryodes Solanaceae.Duckeodendron
## [5] Solanaceae.Markea Solanaceae.Solanum
## [7] Sapindaceae.Allophylastrum Sapindaceae.Cupania
## [9] Sapindaceae.Thinouia Rubiaceae.Psychotria
## [11] Rubiaceae.Duroia Rubiaceae.Cinchona
## [13] Lauraceae.Ocotea Lauraceae.Licaria
## [15] Lauraceae.Rhodostemonodaphne Anisophylleaceae.Anisophyllea
## [17] Pentaphylacaceae.Freziera
## 119 Levels: Anisophylleaceae.Allophylastrum ... Solanaceae.Trattinnickia
Essa função computa um vetor de fatores que representa a interação das colunas fornecidas na tabela 1. Se fizermos isso com a tabela 3, poderemos saber quais combinações ocorrem em ambas as tabelas.
interaction(tab3[, chaves])
## [1] Burseraceae.Protium Burseraceae.Trattinnickia
## [3] Burseraceae.Dacryodes Sapindaceae.Allophylastrum
## [5] Sapindaceae.Cupania Sapindaceae.Thinouia
## 12 Levels: Burseraceae.Allophylastrum ... Sapindaceae.Trattinnickia
Agora utilizamos a mesma função interaction e o operador %in% para retornar um vetor lógico que utilizaremos para filtrar os valores da tabela 1 com correspondência na tabela 3.
linhas <- interaction(tab1[, chaves]) %in% interaction(tab3[, chaves])
linhas
## [1] TRUE TRUE TRUE FALSE FALSE FALSE TRUE TRUE TRUE FALSE FALSE FALSE
## [13] FALSE FALSE FALSE FALSE FALSE
tab1[linhas,]
## familia genero epiteto
## 1 Burseraceae Protium aracouchini
## 2 Burseraceae Trattinnickia burserifolia
## 3 Burseraceae Dacryodes edilsonii
## 7 Sapindaceae Allophylastrum frutescens
## 8 Sapindaceae Cupania rubiginosa
## 9 Sapindaceae Thinouia myriantha
Antijunção
retorna todas as linhas de
xem que não há correspondência emy, mantendo apenas colunas dex.
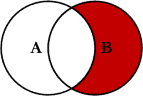
Uma antijunção é ligeiramente diferente de uma semijunção pois ela retorna todas as linhas de x que não aparecem em y.
Portanto, podemos utilizar o inverso de nosso vetor lógico linhas e utilizar este inverso para filtrar as linhas da tabela 1 e ter nossa tabela antijunção entre x e y:
antilinhas <- !linhas
tab1[antilinhas, ]
## familia genero epiteto
## 4 Solanaceae Duckeodendron cestroides
## 5 Solanaceae Markea ulei
## 6 Solanaceae Solanum cyathophorum
## 10 Rubiaceae Psychotria viridis
## 11 Rubiaceae Duroia eriopila
## 12 Rubiaceae Cinchona amazonica
## 13 Lauraceae Ocotea delicata
## 14 Lauraceae Licaria aureosericea
## 15 Lauraceae Rhodostemonodaphne recurva
## 16 Anisophylleaceae Anisophyllea manausensis
## 17 Pentaphylacaceae Freziera carinata
Para saber mais
- Join in R;
- Tudo sobre Joins (merge) em R;
- Join com dplyr;
- Entendendo o JOIN do SQL (ou Junções) - Obtive as imagens aqui apresentadas desta página. Há uma boa explicação com SQL como pano de fundo para operações de junções de tabela.
Referências
APG. 2016. “An update of the Angiosperm Phylogeny Group classification for the orders and families of flowering plants: APG IV.” Botanical Journal of the Linnean Society 181: 1–20.
- Posted on:
- April 23, 2020
- Length:
- 12 minute read, 2469 words
- Tags:
- R Tutorial BOT89 junção de tabelas base R